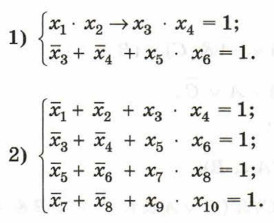|
|
|
|
|
Самое главное. Вопросы и задания § 20. Преобразование логических выраженийСамое главное Способ определения истинности логического выражения путём построения его таблицы истинности становится неудобным при увеличении количества логических переменных, т. к. за счёт существенного увеличения числа строк таблицы становятся громоздкими. В таких случаях выполняются преобразования логических выражений в равносильные. Для этого используют свойства логических операций, которые иначе называют законами алгебры логики. Аналогичные законы имеют место и в алгебре множеств. Логическая функция может быть задана с помощью таблицы истинности или аналитически, т. е. с помощью логического выражения. Для всякой таблицы истинности можно составить соответствующее ей логическое выражение. Вопросы и задания 1. Какие из рассмотренных законов алгебры логики аналогичны законам алгебры чисел, а какие нет? 2. Докажите второй закон де Моргана с помощью таблиц истинности. 3. Путём преобразования докажите равносильность следующих высказываний:
4. Упростите логические формулы:
*5. Найдите X, если
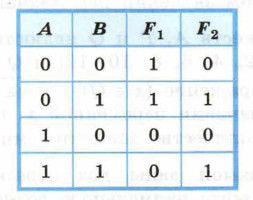
12. Сколько существует различных логических функций от четырёх переменных? 13. По заданной таблице истинности составьте логические выражения для функций F1, F2.
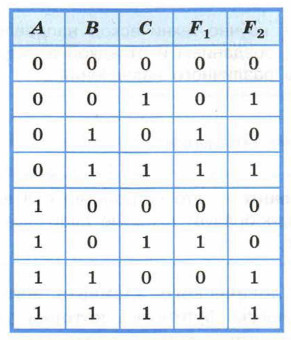
14. По известным таблицам истинности запишите аналитическое представление импликации, эквиваленции и строгой дизъюнкции. 15. Логические функции штрих Шеффера и стрелка Пирса названы так в честь математиков, исследовавших их свойства. Подготовьте краткую биографическую справку об одном из этих учёных. 16. По заданной таблице истинности составьте логические выражения для функций F1, F2.
17. Запишите логическое выражение для логической функции F(A, В, С), равной 1 на наборах 011, 101, 110, 111. Попытайтесь упростить полученное выражение.
|
|
|



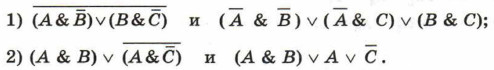
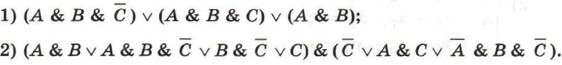
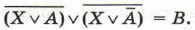
 6. На числовой прямой даны два отрезка: Р = [10; 25] и Q = [20; 55]. Укажите наибольшую возможную длину такого отрезка А, что выражение
6. На числовой прямой даны два отрезка: Р = [10; 25] и Q = [20; 55]. Укажите наибольшую возможную длину такого отрезка А, что выражение  истинно при любом значении переменной х.
истинно при любом значении переменной х.
 истинно при любом значении переменной х. Определите наименьшее возможное количество элементов множества А.
истинно при любом значении переменной х. Определите наименьшее возможное количество элементов множества А.
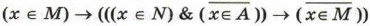 истинно при любом значении переменной х.
истинно при любом значении переменной х.
 тождественно истинно, т. е. принимает значение 1 при любом натуральном значении десятичной переменной х. (Здесь & — поразрядная конъюнкция двух неотрицательных целых десятичных чисел.)
тождественно истинно, т. е. принимает значение 1 при любом натуральном значении десятичной переменной х. (Здесь & — поразрядная конъюнкция двух неотрицательных целых десятичных чисел.)