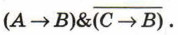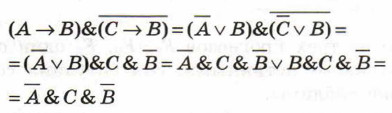|
|
|
|
|
§ 22. Логические задачи и способы их решения Решение логических задач путём упрощения логических выраженийСледующий формальный способ решения логических задач состоит в том, чтобы: 1) выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами; 2) записать условие задачи на языке алгебры логики, соединив простые высказывания в составные с помощью логических операций; 3) составить единое логическое выражение, учитывающее все требования задачи; 4) используя законы алгебры логики, упростить полученное выражение и вычислить его значение; 5) выбрать решение — набор логических переменных (элементарных высказываний), при котором построенное логическое выражение является истинным; 6) убедиться, что полученное решение удовлетворяет всем условиям задачи.
Обозначим через А, В, С простые высказывания:
Из условия задачи следует истинность высказывания:
Упростим получившееся высказывание:
Получившееся высказывание будет истинным только в случае, если С — истина, а А и В — ложь. А это значит, что логику изучал только третий ученик, а первый и второй не изучали.
|
|
|



 Пример 7. На вопрос, кто из трёх учащихся изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из учащихся изучал логику?
Пример 7. На вопрос, кто из трёх учащихся изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из учащихся изучал логику?