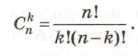Главная >> Информатика 10 класс. Босова

§ 4. Обработка информации

Кодирование информации

Кодирование информации широко используется в технических средствах работы с информацией (телеграф, радио, компьютеры).

Кодирование — это обработка информации, заключающаяся в её преобразовании в некоторую форму, удобную для хранения, передачи, обработки информации в дальнейшем. Код — это система (список) условных обозначений (кодовых слов), используемых для представления информации1. Кодовая таблица — это совокупность используемых кодовых слов и их значений.

¹ Также кодом зачастую называют результат кодирования информации.

Ранее мы уже рассмотрели примеры равномерных двоичных кодов — пятиразрядный код Бодо и восьмиразрядный код ASCII.

Самый известный пример неравномерного кода — код (азбука) Морзе, в которой цифры и буквы алфавита представляются последовательностями длинных («тире») и коротких («точек») сигналов, названный в честь американского изобретателя и художника Сэмюэля Морзе (1791-1872). Буквы, встречающиеся в сообщениях чаще, имеют в этом коде более короткий код, чем «редкие» буквы (рис. 1.12).

В азбуке Морзе сигналы отделяются друг от друга паузами — отсутствием сигналов. За единицу «измерения» длительности сигналов принимается длительность сигнала «точка». Длительность тире (длинного сигнала) равна длительности трёх точек (коротких сигналов). Пауза между сигналами одного знака равна одной точке; пауза между знаками в слове — трём точкам; пауза между словами — семи точкам. Фактически пауза является третьим знаком в азбуке Морзе, а сам код — троичным.

Слово WORD, закодированное с помощью азбуки Морзе, на «временной» шкале можно представить так:

Самым знаменитым сообщением, закодированным азбукой Морзе, является сигнал бедствия «SOS». Его запрещено использовать без острой на то необходимости. Передаётся сигнал без межбуквенных пауз:

При использовании неравномерных кодов важно понимать, сколько различных кодовых слов они позволяют построить.

Пример 1. Светодиодная панель содержит восемь излучающих элементов, каждый из которых может светиться или красным, или жёлтым, или синим, или зелёным цветом. Сколько различных сигналов можно передать с помощью панели (все излучающие элементы должны гореть, порядок цветов имеет значение)?

На уроках математики и информатики в основной школе вы изучали элементы комбинаторики, в том числе правило умножения. Согласно ему, если элемент А можно выбрать n способами и при любом выборе А элемент В можно выбрать m способами, то пару (А, В) можно выбрать n • m способами. Это правило справедливо и для произвольного количества независимо выбираемых элементов.

Применим его к решению нашей задачи.

Существует 4 варианта выбора цвета первого элемента, 4 варианта выбора цвета второго элемента; цвета для пары элементов (1, 2) можно выбрать 4 • 4 = 4² = 16 способами; цвета для тройки элементов (1, 2, 3) можно выбрать 16 • 4 = 4³ = 64 способами и т. д. Цвета для восьми элементов (1, 2, 3, 4, 5, 6, 7, 8) можно выбрать 4⁸ = 65 536 способами.

Можно ли отнести эту задачу к классу задач на определение максимально возможного количества комбинаций (слов) фиксированной длины определённого алфавита? Обоснуйте свой ответ.

Пример 2.

Выясним, сколько всего различных символов можно закодировать, используя последовательности точек и тире, содержащие не более шести знаков.

Для кодирования различных символов можно использовать последовательности точек и тире, содержащие не более шести знаков, т. е. 1, 2, 3, 4, 5 или 6 знаков.

Последовательностями, содержащими один из двух возможных знаков, можно закодировать два символа: один будет закодирован точкой, второй — тире.

Рассмотрим последовательности, содержащие два знака из двухсимвольного алфавита. Их может быть 2 • 2 = 2² = 4.

Последовательностей из трёх знаков, принадлежащих двухсимвольному алфавиту, может быть 4 • 2 = 2³ = 8.

Рассуждая аналогичным образом, подсчитаем число последовательностей, содержащих 4, 5 и 6 знаков — 16, 32 и 64 соответственно.

Число различных последовательностей, содержащих не более шести знаков двухсимвольного алфавита, будет равно 126 = 2 + 4 + 8 + 16 + 32 + 64.

Пример 3.

Имеющаяся информация должна быть закодирована в четырёхбуквенном алфавите {А, В, С, D}. Выясним, сколько существует различных последовательностей из 7 символов четырёхбуквенного алфавита {А, В, С, D}, которые содержат ровно пять букв А.

Нас интересуют семисимвольные последовательности, любые пять мест в которых будут заняты буквой А, а на двух оставшихся местах могут находиться любые из букв В, С, D.

Например:

Так как на 6-м и 7-м местах могут стоять любые из трёх оставшихся букв В, С, D, то всего существует 9 (3 • 3 = 9) разных семибуквенных последовательностей, в которых первые пять позиций заняты буквой А.

Но ведь буквы А могут находиться на любых пяти из имеющихся семи позиций. Например:

А сколько таких вариантов всего? Сколько всего существует способов, которыми мы можем выбрать пять мест из семи для размещения там буквы А?

Для ответа на этот вопрос нужно вспомнить некоторые сведения из изученного в основной школе раздела математики, называемого комбинаторикой.

В комбинаторике набор k элементов, выбранных из данного множества, содержащего n различных элементов, называется сочетанием из n по k.

Для вычисления значения этой величины применяется формула:

Здесь n! = 1 • 2 • ... • n.

Окончание >>>