|
|
|
|
|
§ 4. Обработка информации 4.2. Кодирование информацииДействительно, множество, с которым мы имеем дело, состоит из мест для записи символов в последовательности. Его элементы можно обозначить 1, 2, 3, 4, 5, 6 и 7. Требуется выбрать из этого множества пять мест для размещения буквы А. Число возможных вариантов можно вычислить как число сочетаний из 7 по 5:
Итак, существует 21 вариант выбора в семибуквенной последовательности ровно пяти мест для размещения там буквы А. Для каждого из этих 21 вариантов имеется 9 разных вариантов заполнения двух оставшихся мест. Всего существует 189 (21 • 9 = 189) различных последовательностей из 7 символов четырёхбуквенного алфавита {А, В, С, D}, которые содержат ровно пять букв А. Главное условие использования неравномерных кодов — возможность однозначного декодирования записанного с их помощью сообщения. Именно поэтому в технических системах широкое распространение получили префиксные коды: они состоят из слов разной длины, записываемых без разделительного символа. При этом сообщение, закодированное с их помощью, может быть однозначно декодировано.
Например: 1) код, состоящий из слов 0, 10 и 11, является префиксным;
Для того чтобы сообщение, записанное с помощью неравномерного кода, однозначно декодировалось, достаточно, чтобы никакое кодовое слово не было началом другого (более длинного) кодового слова. Это условие ещё называют условием Фано (в честь Роберта Марио Фано, американского учёного, известного по работам в области теории информации). Обратное условие Фано также является достаточным условием однозначного декодирования неравномерного кода. В нём требуется, чтобы никакой код не был окончанием другого (более длинного) кода.
Выясним, какое сообщение (какой набор букв) закодировано с помощью этих кодов двоичной строкой: 0110100011000. Проанализируем имеющиеся коды: код буквы В (01) является началом кода буквы Е (011); код буквы D (10) является началом кода буквы С (100). Таким образом, прямое условие Фано для заданных кодов не выполняется. Следовательно, имеющуюся двоичную строку нельзя декодировать однозначно, если начать её декодирование с начала (слева направо).
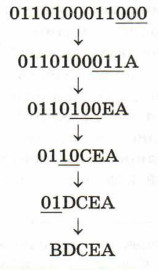
Для имеющихся кодов выполняется обратное условие Фано: никакой код не является окончанием другого кода. Следовательно, имеющуюся двоичную строку можно декодировать однозначно, если начать её декодирование с конца (справа налево). Итак, направление однозначного декодирования установлено. Процесс декодирования может быть представлен так:
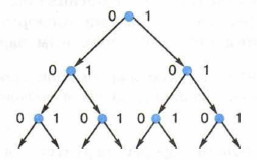
Из курса информатики основной школы вам знакомо понятие дерева — иерархической структуры, состоящей из набора вершин и рёбер. Вершина, в которую не входит ни одного ребра, называется корнем; вершины, из которых не выходит ни одного ребра, называются листьями. Дерево, из вершин которого выходит только два ребра, называется двоичным (бинарным) деревом. Комбинации, соответствующие листьям бинарного дерева, являются кодовыми комбинациями префиксного кода.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В и Г, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Для букв А, Б и В использовали такие кодовые слова: А - 0, Б - 10, В - 110. Каким кодовым словом может быть закодирована буква Г? Код должен удовлетворять свойству однозначного декодирования. Если можно использовать более одного кодового слова, укажите кратчайшее из них. Для решения задачи воспользуемся бинарным деревом.
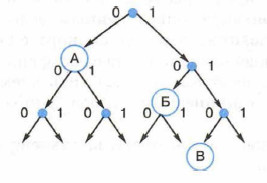
Отметим вершины, соответствующие используемым кодовым словам: А - 0, Б - 10, В - 110:
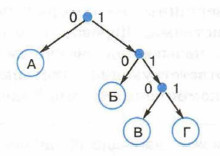
Так как комбинациям префиксного кода должны соответствовать листья бинарного дерева, наше кодовое дерево должно выглядеть так:
Итак, для кодирования буквы Г можно использовать код 111.
Какими кодовыми словами могут быть закодированы буквы Г и Д? Код должен удовлетворять свойству однозначного декодирования. Общая длина кодовых слов для всех пяти букв должна быть минимальной.
|
|
|




 Префиксный код — код со словом переменной длины, обладающий тем свойством, что никакое его кодовое слово не может быть началом другого (более длинного) кодового слова.
Префиксный код — код со словом переменной длины, обладающий тем свойством, что никакое его кодовое слово не может быть началом другого (более длинного) кодового слова.
 Как вы понимаете смысл этого утверждения? Можно ли на его основе заявлять, что если для некоторого кода условие Фано не выполняется, то однозначное декодирование записанного с его помощью сообщения невозможно?
Как вы понимаете смысл этого утверждения? Можно ли на его основе заявлять, что если для некоторого кода условие Фано не выполняется, то однозначное декодирование записанного с его помощью сообщения невозможно?
 Пример 4. Двоичные коды для 5 букв латинского алфавита представлены в таблице:
Пример 4. Двоичные коды для 5 букв латинского алфавита представлены в таблице:

 Пример 5.
Пример 5.